Einfluss der Stoffmenge
Nach dem Kollisionsmodell müssen sich Teilchen treffen um miteinander reagieren zu können.
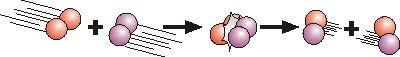
z.B. H2 + I2 → 2 HI
Es leuchtet ein, dass die Anzahl der Kollisionen pro Zeiteinheit - und damit die Reaktionsgeschwindigkeit - proportional zur Konzentration der Reaktionspartner ist. Die Anzahl der Kollisionen, die prinzipiell eine Reaktion ermöglichen, kann berechnet werden.
Mathematisch wird ein proportionaler Zusammenhang durch eine Multiplikation ausgedrückt. So ist z.B. die Menge des veratmeten Sauerstoffs in einem Raum pro Zeiteinheit proportional zur Anzahl der anwesenden Personen (NP). Die Geschwindigkeit, mit der Sauerstoff verbraucht wird (vSV ), kann dann unter Verwendung eines konstanten, mittleren Sauerstoffverbrauchs pro Person und Zeiteinheit (KSVP) folgendermaßen berechnet werden:
![]()
Die mathematische Beschreibung der Reaktionsgeschwindigkeit durch Multiplikation (und nicht z.B. durch Addition) kann auch daran nachvollzogen werden, dass die Reaktionsgeschwindigkeit auch dann Null sein muss, wenn zwar einer der Reaktionspartner in sehr großer Konzentration vorliegt, der andere jedoch gar nicht vorhanden, seine Konzentration also Null ist.
Analog zum Sauerstoffverbrauch kann auch die Reaktionsgeschwindigkeit (vR , Änderung der Iodwasserstoffkonzentration pro Zeit, d[HI]/dt) der oben gezeigten bimolekularen Reaktion von Wasserstoff mit Iod in Abhängigkeit von deren Konzentrationen ([H2] und [I2]) beschrieben werden:
![]() K steht hierbei für die Geschwindigkeitskonstante
K steht hierbei für die Geschwindigkeitskonstante
Die Geschwindigkeitskonstante trägt z.B. der Tatsache Rechnung, dass nicht jede Kollision auch zur Reaktion führt, da z.B. die Orientierung der Teilchen nicht stimmt. Die Geschwindigkeitskonstante muss experimentell bestimmt werden. Misst man für die oben angeführte Reaktion die Reaktionsgeschwindigkeit als Änderung der Konzentration des entstehenden Iodwasserstoffs z.B. pro Sekunde, so geht man dazu prinzipiell folgendermaßen vor:
Bekannte Konzentrationen von Iod und Wasserstoff werden zur Reaktion gebracht, nach einer Sekunde (oder kontinuierlich) wird dann die Menge des entstandenen Iodwasserstoffs bestimmt. Setzt man in die obige Gleichung nun sowohl die anfänglichen Iod- und Wasserstoffkonzentrationen, als auch die nach einer Sekunde bestimmte Iodwasserstoffkonzentration ein, so kann man den Wert der Geschwindigkeitskonstante K berechnen.
Reaktionen bei denen nicht nur zwei, sondern drei Teilchen kollidieren, werden als trimolekulare Reaktionen bezeichnet. Die mathematische Beschreibung der Reaktionsgeschwindigkeit von trimolekularen Reaktionen erfolgt sehr ähnlich. Die Reaktionsgeschwindigkeit ist in diesem Fall von der Konzentration aller drei Reaktionspartner abhängig.